Physics - භෞතික විද්යාව කෙටි සටහන් - 2 (තුන්වන කොටස)
දෙවන ඒකකය - යාන්ත්ර විද්යාව ( Mechanics )
තුන්වන කොටස
කාර්යක්ෂමතාවය ( Efficiency )
- ඒකක නැත.
- මාන නැත.
- අදිශ රාශියකි.
කාර්යක්ෂමතාවය = Wout × 100% / Win
අයින්ස්ටයින්ගේ ශක්ති ස්කන්ධ සම්බන්ධය ( Einstein's Mass Energy Relation Ship )
- අයින්ස්ටයින්ගේ පැහැදිලි කිරීම් වලට අනුව ස්කන්ධය යනු ඒකරාශි වූ ශක්තිය යි. සුදුසු යාන්ත්රණයක් මගින් ස්කන්ධය විනාශ කළ විට නිදහස් වන ශක්ති ප්රමාණය E නම්,
E = mc2
- මෙහි යෙදෙන C රික්තය තුළදී ආලෝකයේ ප්රවේගය 3×108 ms-1 වේ.
වෘත්ත චලිතය ( Circular Motion )
අංශුවක් වෘත්තාකාර මාර්ගයක ගමන් කරවීම සඳහා
- ස්පර්ශකයේ දිශාවට ප්රවේගයක් ලබා දිය යුතුය.
- කේන්ද්රය දෙසට සම්ප්රයුක්ත බලයක් පවත්වා ගත යුතුයි.
කෝණික විස්ථාපනය ( Angular Displacement )
- ඒකක - rad
- මාන නැත.
- අදිශ රාශියකි.
කෝණික විස්ථාපන වෙනස,
- ඒකක - rad
- මාන නැත.
- දෛශික රාශියකි.
විස්ථාපන වෙනස (θ) = θපසු - θපෙර
කෝණික ප්රවේගය ( Angular Velocity )
- ඒකක - rads-1
- මාන - T-1
- දෛශික රාශියකි. (වෘත්තයේ තලයට ලම්බකව තලය තුලට හෝ ඉන් ඉවතට.)
ආවර්ත කාලය ( Periodic Time )
- නියත කෝණික ප්රවේගයකින් වෘත්තාකාර මාර්ගයක ගමන් කරන අංශුවක් සම්පූර්ණ වටයක් ගෙවා නිම කිරීමට ගත කරන කාලය ආවර්ත කාලය ලෙස හඳුන්වයි.
T = 2π / ω
සංඛ්යාතය ( Frequency )
නියත කෝණික ප්රවේගයකින් වෘත්තාකාර මාර්ගයක ගමන් කරන අංශුවක් තත්පර 1කදී ගෙවා යන වට ගණන සංඛ්යාතය ලෙස හදුන්වයි.
- ඒකක - S-1, Hz, ω = 2πf
- මාන - T-1
- අදිශ රාශියකි.
කෝණික ත්වරණය ( Angular Acceleration )
- ඒකක - rads-2
- මාන - T-2
- දෛශික රාශියකි. (වෘත්තයේ තලයට ලම්බකව පවතී.)
යම් මොහොතකදී ත්වරණය යනු අරීය ත්වරණයේත් ස්පර්ශීය ත්වරණයේත් සම්ප්රයුක්තය වේ.
α = Δω / Δt
ω = ω0 + αt
θ = (ω0 + ω) t / 2
θ = ω0t + (αt2 / 2 )
ω2 = ω02 + 2αθ
ω0 - ආරම්භක කෝණික ප්රවේගය
ω - අවසාන කෝණික ප්රවේගය
α - කෝණික ත්වරණය
θ - කෝණික විස්ථාපනය
t - කාලය
අරීය ත්වරණය ( Radial Acceleration )
ar = vω
ar = Rω2
ar = v2 / R
v - රේඛීය ප්රවේගය
ω - කෝණික ප්රවේගය
R - අරය
වෘත්ත චලිතය හා උත්තාරණ චලිතය ( Mean Angular Velocity )
ω = (ω0 + ω) / 2
ω = (θ1+θ2+θ3+...) / (t1+t2+t3+...)
භ්රමණ චලිතය ( Rotational Motion )
- දෘඩ වස්තුවක් යම් අක්ෂයක් වටා භ්රමණය වන විට එම අක්ෂය භ්රමණ අක්ෂය ලෙස හඳුන්වයි. භ්රමණ අක්ෂයට ලම්භක තලය භ්රමණ තලය ලෙස හඳුන්වයි.
අවස්ථිති ඝූර්ණය ( Moment Of Inertia )
- ඒකක - kgm2
- මාන - ML2
- අදිශ රාශියකි.
I = Σ mr2
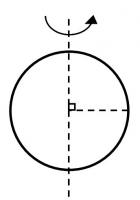 අංශුවක I = mr2
අංශුවක I = mr2 වෘත්ත වළල්ලක I = mr2
වෘත්ත වළල්ලක I = mr2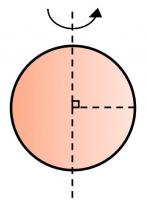 වෘත්ත ආස්තරයක I = mr2 / 2
වෘත්ත ආස්තරයක I = mr2 / 2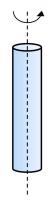 සිලින්ඩරාකාර කබොලක I = mr2
සිලින්ඩරාකාර කබොලක I = mr2 ඝන සිලින්ඩරයක I = mr2 / 2
ඝන සිලින්ඩරයක I = mr2 / 2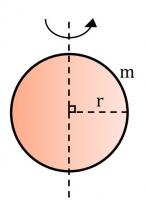 ගෝලීය කබොලක I = 2mr2 / 3
ගෝලීය කබොලක I = 2mr2 / 3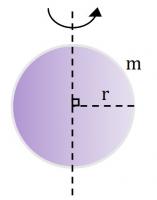 ඝන ගෝලයක I = 2mr2 / 5
ඝන ගෝලයක I = 2mr2 / 5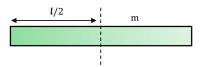 ඍජු දණ්ඩක I = ml2 / 12
ඍජු දණ්ඩක I = ml2 / 12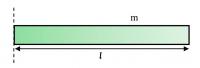 ඍජු දණ්ඩක I = ml2 / 3
ඍජු දණ්ඩක I = ml2 / 3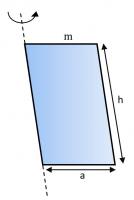 දොරක I = ma2 / 3
දොරක I = ma2 / 3
- සංයුක්තයක් යම් අක්ෂයක් වටා භ්රමණය වන විට භ්රමණ අක්ෂය වටා සංයුත්තයේ අවස්ථිති ඝූර්ණය, භ්රමණ අක්ෂය වටා එක් එක් වස්තුව ඇති කරන අවස්ථිති ඝූර්ණයන්ගේ එකතුවට සමාන වේ.
කෝණික ගම්යතාව ( Angular Momentum )
- ඒකක - kgm2rads-1
- මාන - ML2T-1
- දෛශික රාශියකි. (භ්රමණ අක්ෂය ඔස්සේ පවතී.)
L = Iω
- දෘඪ වස්තුවක් භ්රමණය වන විට භ්රමණ අක්ෂය වටා එක් එක් අංශුවේ රේඛීය ගම්යතා ඝූර්ණය සොයා ඒවා සියල්ල එකතු කිරීමෙන් ද භ්රමණ අක්ෂය වටා කෝණික ගම්යතාවය ලබාගත හැකිය.
කෝණික ගම්යතා සංස්ථිති නියමය...
භ්රමණය වන වස්තුවක් හෝ පද්ධතියක් මත සම්ප්රයුක්ත ව්යාවර්තයක් ක්රියා නොකරන දිශාවට ඇති සම්ප්රයුක්ත කෝණික ගම්යතාවය සංස්ථිතික වේ.
- මෙයින් අදහස් වන්නේ සම්ප්රයුක්ත කෝණික ගම්යතාවය වෙනස් නොවන බවයි. පද්ධතියේ ඇති එක් වස්තුවක කෝණික ගම්යතාව වැඩි වී අනෙකෙහි ඒ හා සමාන ප්රමාණයකින් අඩුවී සම්ප්රයුක්තය වෙනස් නොවී තිබිය හැක.
භ්රමණ චාලක ශක්තිය ( Rotational Kinetic Energy )
E = Iω2 / 2
E = Lω / 2
E = L2 / 2I
- ලිස්සීමකින් තොරව පෙරලෙන වස්තුවක උත්තාරණ චාලක ශක්තිය අවස්ථිති ඝූර්ණයේ සංගුණකයෙන් ගුණ කළ විට භ්රමණ චාලක ශක්තිය ලැබේ.
ව්යාවර්තය ( Torque )
- ඒකක - Nm
- මාන - ML2T-2
- දෛශික රාශියකි
τ = Iα
τ - ව්යාවර්තය
I - අවස්ථිති ඝූර්ණය
α - කෝණික ත්වරණය
ව්යාවර්තයක් මගින් කරනු ලබන කාර්යය ( Work Done By Torque )
ω = τθ
- කුමන සූත්රයක් මගින් ගණනය කල ද කාර්යයේ SI ඒකක J වේ.
ක්ෂමතාවය ( Power )
P = කාර්යය (W) / කාලය (t)
P = ව්යාවර්තය (τ) × කෝණික ප්රවේගය (ω)
⇒ දෙවන ඒකකයේ දෙවන කොටසට පිවිසීමට ක්ලික් කරන්න. ⇐
⇒ දෙවන ඒකකයේ හතරවන කොටසට පිවිසීමට ක්ලික් කරන්න. ⇐
.. Sithija Ranasingha ..
https://horizonsl.blogspot.com
sithija1996design@gmail.com